TOPIC 2.2
Digital Circuits and Logic Gates

Introduction

In the late 1930s, a young M.I.T. graduate student named Claude Shannon noticed an analogy between the operations of switching devices, such as telephone switching circuits, and the operations of logical connectives. He used this analogy with striking success to solve problems of circuit design and wrote up his results in his master’s thesis, which was published in 1938.

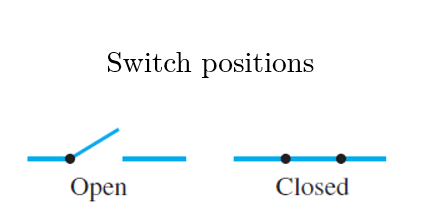
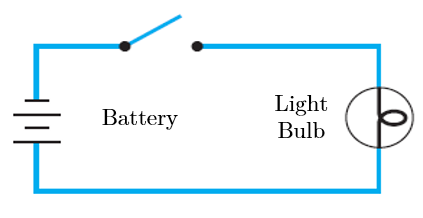
The drawing below (left) shows the appearance of the two positions of a simple switch. When the switch is closed, current can flow from one terminal to the other; when it is open, current cannot flow. Imagine that such a switch is part of the circuit shown below (right). The light bulb turns on if, and only if, current flows through it. And this happens if, and only if, the switch is closed.

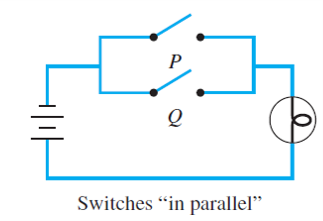
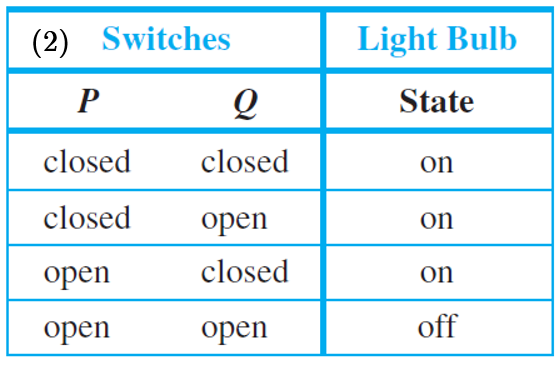
Now consider the more complicated circuits below.

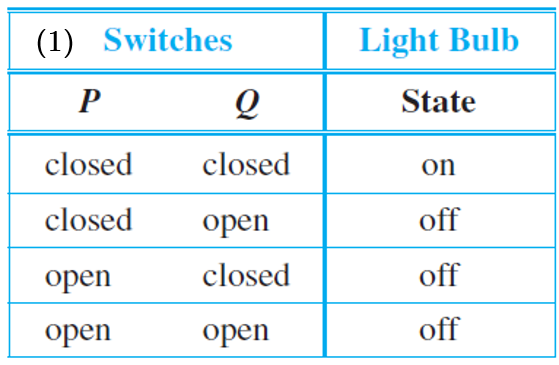
In the circuit above (left), current flows and the light bulb turns on if, and only if, both switches P and Q are closed. The switches in this circuit are said to be in series. In the circuit above (right), current flows and the light bulb turns on if, and only if, at least one of the switches P or Q is closed. The switches in this circuit are said to be in parallel.

Example 1: Construct input/output tables representing the circuits above (1) in series and (2) in parallel.

Observe that if the word "on" is replaced by $$T$$ and "off" is replaced by $$F$$, we obtained the truth tables for "and" and "or". Consequently, the switching circuits are said to correspond to the logical expressions $$P \wedge Q$$ and $$P \vee Q$$.

More complicated circuits corresponds to more complicated logical expressions. Engineers continue to use the language of logic when they refer to values of signals produced by an electronic switch as being "true" or "false". They generally use the symbols 1 and 0 rather than T and F to denote these values. The symbols 0 and 1 are called bits, short for binary digits. This terminology was introduced in 1946 by the statistician John Tukey.

Types of Logic Gates

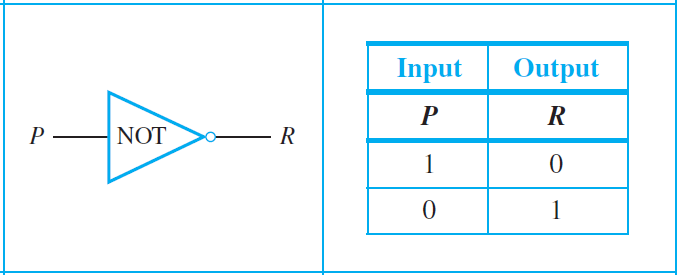
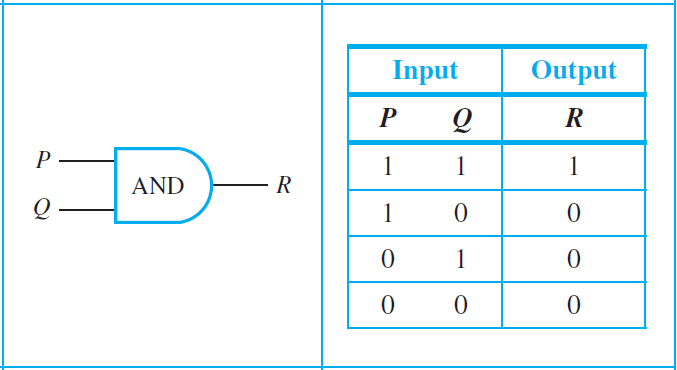
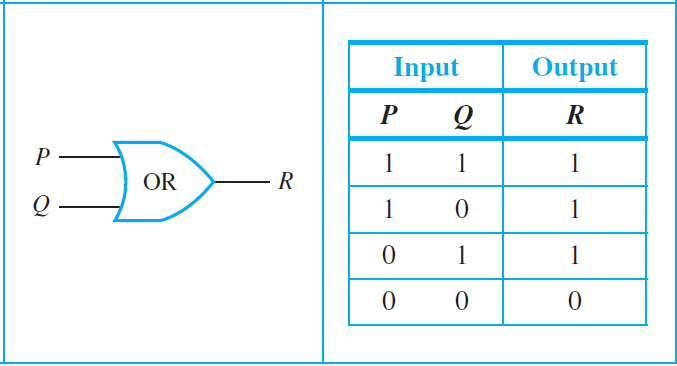
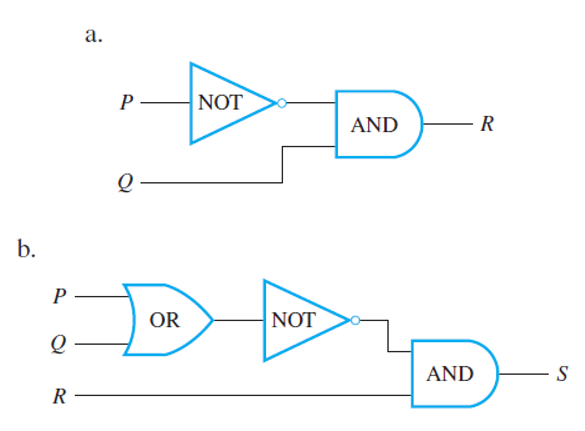
An efficient method for designing more complicated circuits it to build them by connecting less complicated logic gates. Three such gates are known as NOT-gate (or inverter), AND-gate, and OR-gate. The following diagrams summarize their symbolic representations and input/output tables.

Input/Output Tables of Circuits

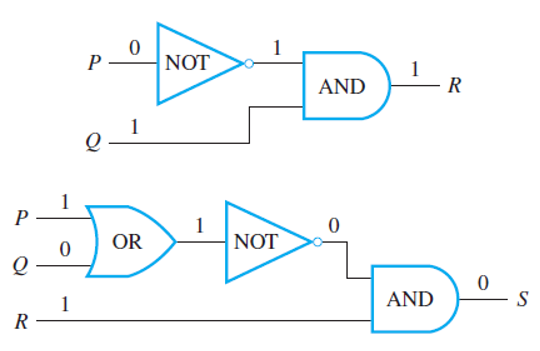
If you are given a set of input signals for a circuit, you can find its output by tracing through the circuit gate by gate. Consider the two circuits below and check the examples that follow.

Example 2: Indicate the output of the above circuits for the given input signals.
Circuit (a) Input signals: $$P = 0$$ and $$Q = 1$$
Circuit (b) Input signals: $$P = 1, Q = 0, R = 1$$

To construct the entire input/output table for a circuit, trace through the circuit to find the corresponding output signals for each possible combination of input signals.

Example 3: Refer to circuit (a) above and construct its input/output table.

Boolean Expressions of Circuits

As noted earlier, One of the founders of symbolic logic was an English mathematician George Boole. In his honor, any variable, such as a statement variable or an input signal, that can take one of only two values is called a Boolean variable. An expression composed of Boolean variables and the connectives $$\sim$$, $$\wedge$$, $$\vee$$ is called Boolean expression.

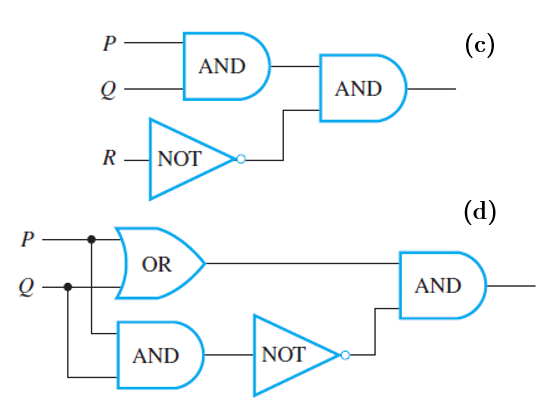
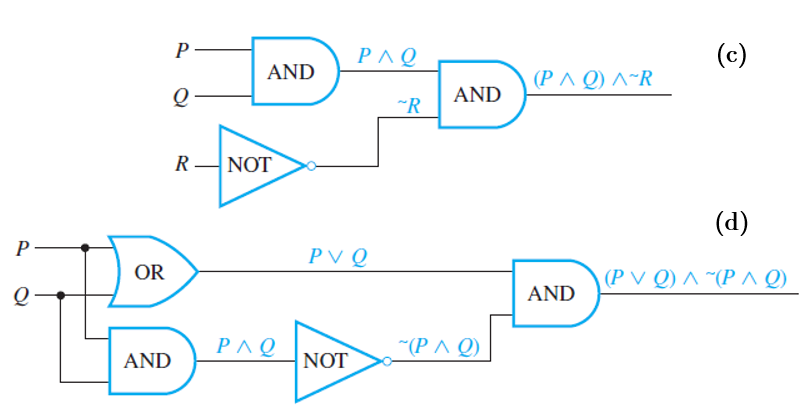
Consider the two circuits below and check the examples that follow.

Example 4: Find the Boolean expressions that correspond to circuits (c) and (d).

The final expression obtained in circuit (d), $$(P ∨ Q)∧ ∼(P ∧ Q)$$, is the expression for exclusive or: P or Q but not both.
For circuit (c), observe that its output is 1 for exactly one combination of inputs $$(P = 1, Q = 1,$$ and $$R = 0)$$ and is 0 for all other combinations of inputs. For this reason, the circuit can be said to “recognize” one particular combination of inputs. The output column of the input/output table has a 1 in exactly one row and 0’s in all other rows.

A recognizer is a circuit that outputs a 1 for exactly one particular combination of input signals and outputs 0's for all other combinations.

Designing Digital Circuits

To costruct a circuit that corresponds to a given Boolean expression:

1. Write the input variables in a column on the left side of the diagram.
2. Then go from the right side of the diagram to the left, working from the outermost part of the expression to the innermost part.
3. Place appropriate gates for every Boolean operator you encounter until all the gates are assigned for the expression placed, arriving at the starting point.

Example 5: Construct a circuit that corresponds to the Boolean expression $$(∼P ∧ Q)∨ ∼Q$$

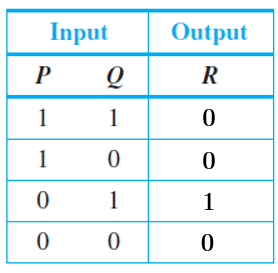
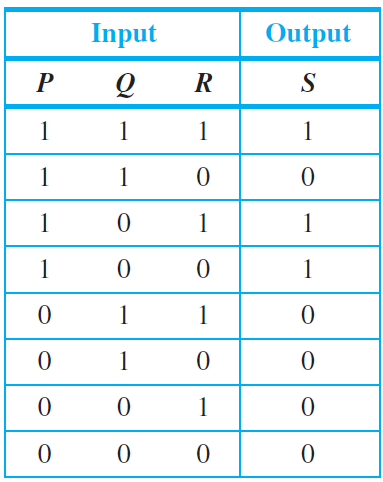
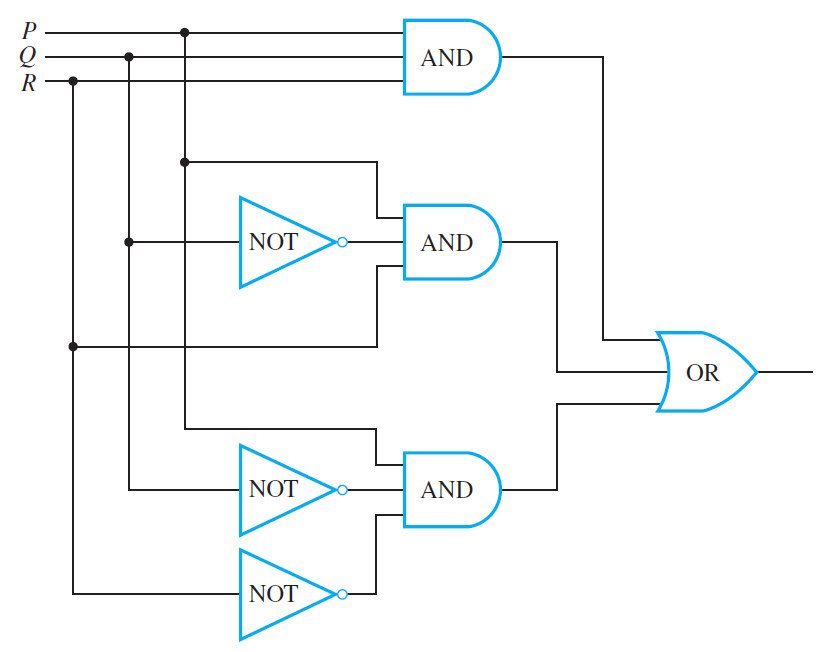
To costruct a circuit that corresponds to a given Input/Output Table, we put several recognizers together in parallel. Specifically, we do the following:

1. Consider only the rows or input combinations that yield an output of 1.
2. For each such row, construct an AND expression of the input states.
3. Once you have the AND expression for all the rows, join them by OR expressions. Enclose each imput combination in a parenthesis to avoid ambiguity in your Boolean expression.
4. Then construct the circuit based on the Boolean expression you obtained.

Consider the truth table below and check the example that follow.

Example 6: Construct a circuit that corresponds to the truth table presented above.

Simplifying Digital Circuits

Aside from being able to design combinatorial circuits, we must know how to simplify or reduce them as well by finding an equivalent circuit or its corresponding Boolean expression. This is where we need to apply the Boolean identities and/or propositional laws to be able to properly modify our Boolean expressions.

Two digital logic circuits are equivalent if, and only if, their input/output tables are identical.

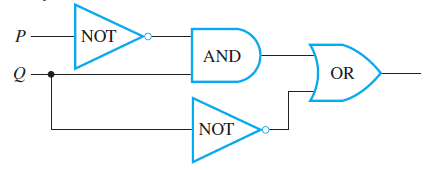
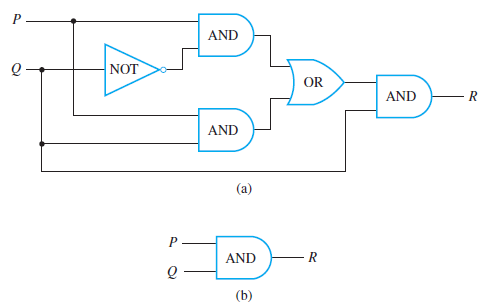
Consider the two circuits below. Construct Input/output tables to compare the behaviors of the two circuits.

As you notice in the two circuits, both of them produce an output of 1 for exactly one imput combination which both of them share: $$P=1$$ and $$Q=1$$. Thus these two circuits do the same job in the sense that they transform the same combinations of input signals. into the same output signals. Yet circuit (b) is simpler than circuit (a) in that it contains many fewer logic gates. Thus, as part of an integrated circuit, it would take less space and require less power.

In other words, since they have equal input/output tables, their Boolean expressions are also concluded to be logically equivalent. In general, you can simplify a combinational circuit by finding the corresponding Boolean expression, using the properties listed in the summary of logical equivalences to find a Boolean expression that is shorter and logically equivalent to it (when both are regarded as statement forms), and constructing the circuit corresponding to this shorter Boolean expression.

Example 7: Refer to the two logically equivalent circuits (a) and (b).
(1) Find the Boolean expressions for each circuit;
(2) Show that these expressions are logically equivalent when regarded as statement forms.

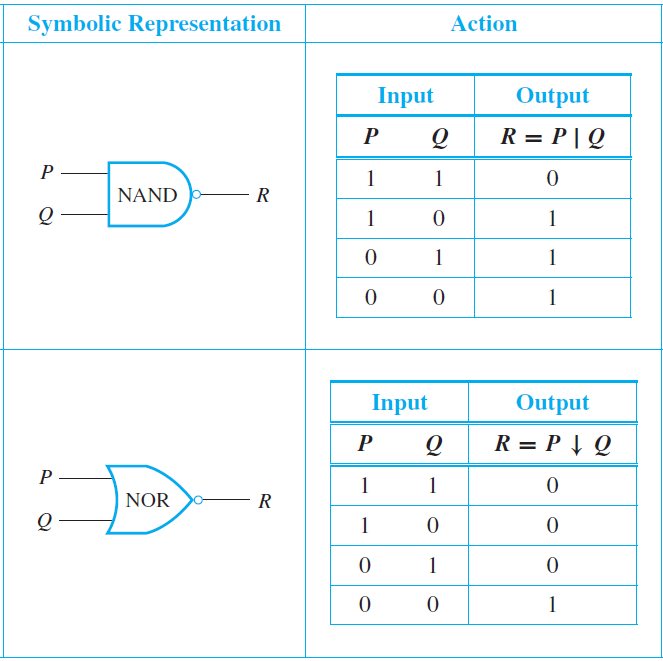
NAND and NOR Gates

Another way to simplify a circuit is to find an equivalent circuit that uses the least number of different kinds of logic gates. Here are some additional useful gates to the ones that are presented earlier:

The table below summarizes the actions of NAND and NOR gates.

It can be shown that any Boolean expression is equivalent to one written entirely with Sheffer strokes or entirely with Peirce arrows. Thus any digital logic circuit is equivalent to one that uses only NAND-gates or only NOR-gates.

Example 8: Use the laws of logical equialence and the definition of Sheffer stroke to show that
(1) $$∼P ≡ P | P$$
(2) $$P ∨ Q ≡ (P | P) | (Q | Q)$$.