Lesson Objectives
- Know and perform the key operations involved in Boolean algebra.
- Derive and familiarize various boolean identities.
- Simplify boolean expressions using boolean identities.
Introduction
George Boole is an English mathematician who helped establish modern symbolic logic and whose algebra of logic, which is currently known as Boolean algebra. Specifically, He found the link between logic and mathematics which now helps prove undiscovered relationships and in the field of electronics, simplify circuits and programs to keep things running efficiently.
Boolean algebra provides the operations and the rules for working with the set {0, 1}. Electronic and optical switches can be studied using this set and the rules of Boolean algebra. Digital computers contain circuits that implement Boolean functions. The simpler the Boolean function, the smaller the circuit. Simpler circuits yield the following benefits: (1) They are cheaper to build, (2) consume less power and resources, and (3) run faster than complex circuits. The main way to do so is to reduce or simplify Boolean functions to their simplest form.
Operations in Boolean Algebra
The three operations in Boolean algebra that we will use most are complementation, the Boolean sum, and the Boolean product.
- The complement of an element, denoted with a bar, is defined by
- The Boolean sum, denoted by $$+$$ or by OR, has the following values:
- The Boolean product, denoted by $$\cdot$$ or by AND, has the following values:
When there is no danger of confusion, the symbol $$·$$ can be deleted, just as in writing algebraic products. Unless parentheses are used, the rules of precedence for Boolean operators are: First, all complements are computed, followed by Boolean products, followed by all Boolean sums.
$$1\cdot 0 + \overline{(0+1)}$$
$$= 0 + \overline{1}$$
$$= 0 + 0$$
$$= 0$$
The complement, Boolean sum, and Boolean product correspond to the logical operators, $$\sim$$, $$\vee$$, and $$\wedge$$, respectively, where 0 corresponds to F (false) and 1 corresponds to T (true). Equalities in Boolean algebra can be directly translated into equivalences of compound propositions. Conversely, equivalences of compound propositions can be translated into equalities in Boolean algebra.
(1) $$(T \wedge F) \vee \sim(T \vee F) \equiv F$$
(2) $$( 1 \cdot 1 ) + \overline{0} = 1$$
Evaluating Boolean Functions
Definition: Let $$B = \left\{0,1\right\}$$. Then
is the set of all possible n-tuples of 0's and 1's. The variable x is called a Boolean variable if it assumes values only from B. A function from $$B^{n}$$ to B is called a Boolean function of degree n.
For instance, The function $$F(x, y) = x\overline{y}$$ from the set of ordered
pairs of Boolean variables to the set $$\left\{0,1\right\}$$ is a Boolean function of
degree 2 with the following values:
$$F(1, 0) = 1 \cdot \overline{0} = 1 \cdot 1 = 1$$
$$F(0, 1) = 0 \cdot \overline{1} = 0 \cdot 0 = 0$$
$$F(0, 0) = 0 \cdot \overline{0} = 0 \cdot 1 = 0$$
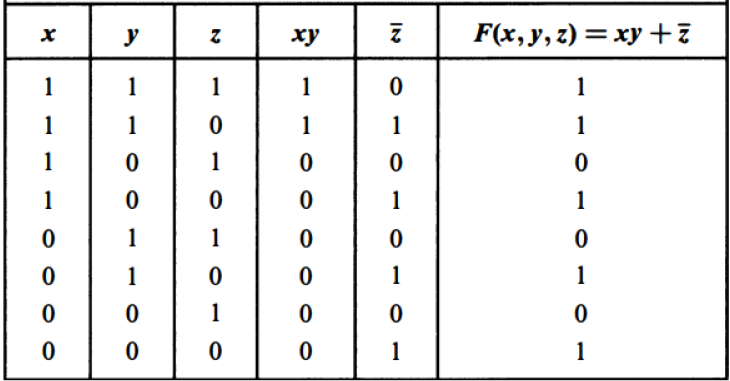
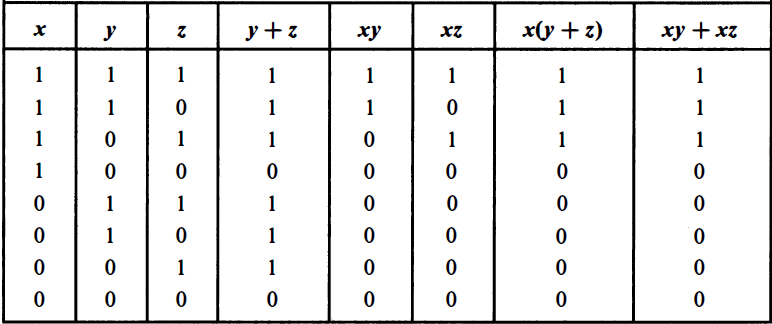
Boolean Identities
The following summarizes the important Boolean identities that can be applied in simplifying boolean expressions. These identities are particularly useful in simplifying the design of circuits later on.
Since the truth values of $$x(y+z)$$ and $$(x+y)(x+z)$$ are equal for all input combinations, it can be concluded
that the equality above is valid.
Simplifying Boolean Expressions
Identities in Boolean algebra can be used to prove further identities. Also, it can be used to manipulate or reduce the complexity of boolean expressions to simplify their equivalent logic circuits.
Study the following examples below.
$$x (x + y)$$
$$= (x + 0)(x + y)$$ - Identity law for Boolean sum
$$= x + 0 \cdot y$$ - Distributive law of Boolean sum over Boolean product
$$= x + y \cdot 0$$ - Commutative law for Boolean product
$$= x + 0$$ - Domination law for Boolean product
$$= x$$ - Identity law for Boolean sum
$$\overline{(\overline{a} \cdot b)} \cdot (a + b)$$
$$= (\overline{\overline{a}} + \overline{b}) \cdot (a + b)$$ - De Morgan's law
$$= (a + \overline{b}) \cdot (a + b)$$ - Double complement law
$$= a + (b \cdot \overline{b})$$ - Distributive law of Boolean sum over Boolean product
$$= a + 0$$ - Zero property of Boolean product
$$= a$$ - Identity law of Boolean sum
Therefore, $$\overline{(\overline{a} \cdot b)} \cdot (a + b)$$ can be reduced to $$a$$.
Questions or clarifications on this topic? Click here to place your feedback. Your messgages will be highly appreciated.