TOPIC 1.2
Conditional Statements

Evaluating Conditional Statements

Conditional Statements

When you make a logical inference or deduction, you reason from a hypothesis to a conclusion. Your aim is to be able to say, “If such and such is known, then something or other must be the case.”

If p and q are statement variables, the conditional of $$q$$ by $$p$$ is “If $$p$$ then $$q$$” or “$$p$$ implies $$q$$” and is denoted $$p \rightarrow q$$. It is false when $$p$$ is true and $$q$$ is false; otherwise it is true. We call $$p$$ the hypothesis (or antecedent) of the conditional and $$q$$ the conclusion (or consequent).

Things to note:

1. A conditional statement that is true by virtue of the fact that its hypothesis is false if often called vacuously true or true by default.
2. In the expression that include $$\rightarrow$$ as well as other logical operators such as $$\wedge$$, $$\vee$$, and $$\sim$$, the order of operation is that $$\rightarrow$$ is performed last.

Example 1a: Construct a truth table for the statement form $$p ∨ ∼q →∼p$$.

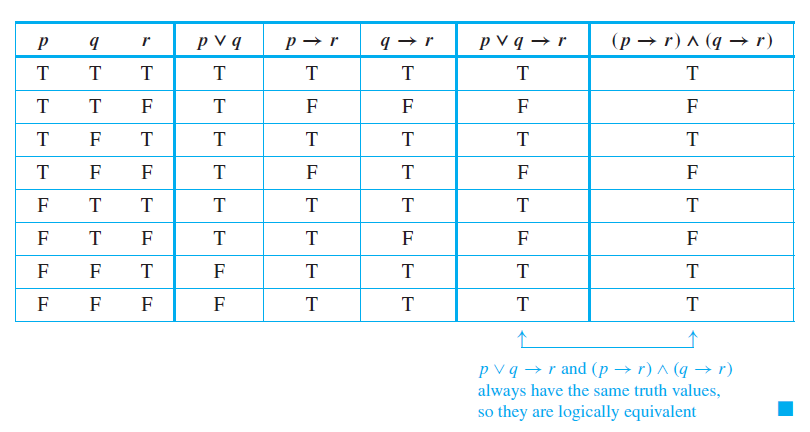
Imagine that you are trying to solve a problem involving three statements: p, q, and r . Suppose you know that the truth of r follows from the truth of p and also that the truth of r follows from the truth of q. Then no matter whether p or q is the case, the truth of r must follow. The division-into-cases method of analysis is based on this idea. See the next example.

Example 1b: Show that $$p ∨ q → r ≡ ( p → r) ∧ (q → r)$$

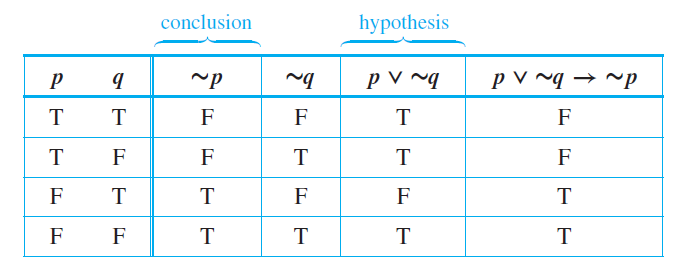
Representation of If-Then as Or

The statement "If p then q" is equivalent to "not p or q". Symbolically, $$p →q ≡ ∼p ∨ q$$.

The logical equivalence of “if p then q” and “not p or q” is occasionally used in everyday speech. Here is one instance.

Example 2: Rewrite the following statement in if-then form: "Either you study for the test or you fail."

Negation of Conditional Statements

By definition, p →q is false if, and only if, its hypothesis, p, is true and its conclusion, q, is false. It follows that the negation of “if p then q” is logically equivalent to “p and not q.” This can be restated symbolically as follows:
$$∼(p →q) ≡ p ∧ ∼q$$

You can also obtain this result by starting from the logical equivalence $$p →q ≡ ∼p ∨ q$$.
Take the negation of both sides to obtain $$∼(p →q) ≡ ∼(∼p ∨ q)$$, which is equivalent to $$∼(∼p) ∧ (∼q)$$ by De Morgan’s laws, which is equivalent to $$p ∧ ∼q$$ by the double negation law.

Example 3: Negate the following statements:
(1) If my car is in the repair shop, then I cannot get to class.
(2) If Sara lives in Athens, then she lives in Greece.

Converse, Inverse, and Contrapositive

Suppose a conditional statement of the form “If p then q” is given
1. The contrapositive is "If ∼q then ∼p"
2. The converse is “If q then p”
3. The inverse is “If ∼p then ∼q”
Symbolically,
The contrapositive of $$p →q$$ is $$∼q →∼p$$.
The converse of $$p →q$$ is $$q → p$$,
and the inverse of $$p →q$$ is $$∼p →∼q$$.

Things to note:

1. A conditional statement is logically equivalent to its contrapositive.
2. A conditional statement and its converse are not logically equivalent.
3. A conditional statement and its inverse are not logically equivalent.
4. The converse and the inverse of a conditional statement are logically equivalent to each other.

Example 4: Write the converse, inverse, and contrapositive of the statement: "If Howard can swim across the lake, then Howard can swim to the island."

Biconditionals

The following expression can be rewritten in two ways: "John will break the world’s record for the mile run only if he runs the mile in under four minutes."

1. If John breaks the world’s record, then he will have run the mile in under four minutes. (Implication)
2. If John does not run the mile in under four minutes, then he will not break the world’s record. (Contrapositive)

Note that it is possible for “p only if q” to be true at the some time that “p if q” is false. For instance, to say that John will break the world’s record only if he runs the mile in under four minutes does not mean that John will break the world’s record if he runs the mile in under four minutes. His time could be under four minutes but still not be fast enough to break the record.

This is where the concept of biconditionals come in.

Given statement variables p and q, the biconditional of p and q is “p if, and only if, q” and is denoted $$p ↔ q$$. It is true if both p and q have the same truth values and is false if p and q have opposite truth values. The words if and only if are sometimes abbreviated iff.

In order of operations, $$↔$$ is coequal with $$→$$. As with $$∧$$ and $$∨$$, the only way to indicate precedence between them is to use parentheses. The full hierarchy of operations for the five logical operators seen below.

1. Evaluate negations $$∼$$ first.
2. Evaluate $$∧$$ and $$∨$$ second. When both are present, parentheses may be needed.
3. Evaluate $$→$$ and $$↔$$ third. When both are present, parentheses may be needed.

Example 5: Show that $$p ↔ q ≡ ( p → q) ∧ (q → p)$$.
Example 6: Rewrite the following statement as a conjunction of two if-then statements: "This computer program is correct if, and only if, it produces correct answers for all possible sets of input data."